3.7 Calor:
3.7.1. Conceito:
É o fluxo (trânsito) de energia entre o sistema
e o meio ambiente, devido a uma diferença de
temperatura.
3.7.2. Convenção de
sinais
Q(+)
 Calor
que entra no sistema
Calor
que entra no sistema
Q(-)
 Calor
que sai no sistema
Calor
que sai no sistema
3.7.3. Calor por
Unidade de Massa (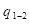 )
)
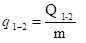
3.7.4. Capacidade
Calorífica (Térmica) de um Sistema

 Capacidade
de um sistema de receber calor em função da
variação da sua temperatura.
Capacidade
de um sistema de receber calor em função da
variação da sua temperatura.
3.7.5. Calor
Específico (Capacidade calorífica Específica)

 Capacidade
de um sistema de receber calor em função da
variação da sua temperatura por unidade de massa
do sistema.
Capacidade
de um sistema de receber calor em função da
variação da sua temperatura por unidade de massa
do sistema.
cp
= calor específico à pressão constante.
cv =
calor específico a volume constante.
3.7.6. Calor Trocado
em um Processo Finito


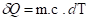
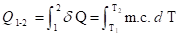
Se “C” e “c” são constantes com a temperatura
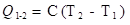
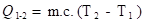
A primeira lei da Termodinâmica, também chamada
de Lei da Conservação da Energia, estabelece
que, durante qualquer ciclo percorrido por um
sistema, o calor efetivo transmitido é igual ao
trabalho efetivo realizado.
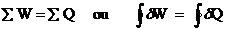

Ex: Uma mola esticada a uma distância de 0,8m é
atada a uma hélice. A hélice, então, gira até
que a mola fique relaxada. Calcule a transmissão
de calor necessária para que o sistema volte a
seu estado inicial.

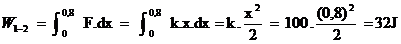
Como retorna ao estado
inicial obtém-se um ciclo
 =
=

A Primeira Lei Aplicada a processos nos quais um
sistema muda de um estado para outro. Podemos
considerar um ciclo composto por dois processos
representados por A e B na figura. Aplicando-se
a primeira lei a esse ciclo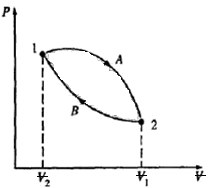
Isso significa que a variação da quantidade Q –W
do estado 1 para o estado 2 é a mesma pelo
caminho A e pelo caminho B. Uma vez que essa
variação é independente do caminho entre os
estados 1 e 2, podemos escrever
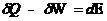
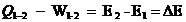

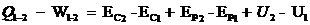
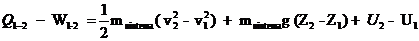
E = Energia do
sistema

U = Energia Interna E
C = Energia Cinética do sistema E P
= Energia Potencial do sistema
ou


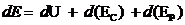



* A
energia interna U é uma propriedade extensiva. A
propriedade intensiva associada a ela é a
energia interna específica u.

* Para sistemas fixos,
referenciais no próprio sistema.
v1 = v2
= 0
z1 = z2
= 0

Exemplo:
Um ventilador de 5 HP é usado em uma sala grande
para promover a circulação de ar. Admitindo que
essa sala é bem isolada do meio e selada,
determine o aumento da energia interna depois de
uma hora de operação.
Por suposição, Q = 0. Como
DEP
= 0 e DEC
= 0, a primeira lei fica –W =
DU.
W = P .
Dt
 W
= (-5 HP).(1 h) . (3600 s/h) = - 1,343 . 107
J
W
= (-5 HP).(1 h) . (3600 s/h) = - 1,343 . 107
J
sinal negativo
Þ sistema recebe trabalho
DU = -
(- 1,343.107) = 1,343.107
ou 13,43 MJ
4.3 ENTALPIA (H)
Na solução de problemas envolvendo
sistemas, certos produtos ou somas de
propriedades ocorrem com regularidade. Uma
combinação de propriedades muito útil será
demonstrada a seguir, considerando a adição de
calor à situação de pressão constante, conforme
a figura abaixo.

O calor é fornecido lentamente ao sistema (gás
em um cilindro), o qual é mantido a uma pressão
constante por um pistão móvel vedado e sem
atrito com o cilindro. Se as variações de
energias cinética e potencial do sistema são
insignificantes e todas as outras formas de
trabalho estão ausentes, a primeira lei requer
que

W = p(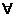 2
-
2
-
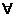 1)
1)
Q = (U2
- U1) + W
Q = (U2 - U1)
+ p(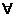 2
-
2
-
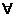 1)
= U2 - U1 +
p
1)
= U2 - U1 +
p
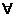 2
- p
2
- p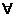 1
1
Q = (U + p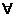 )2
- (U + p
)2
- (U + p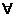 )1
)1

H é uma combinação
de propriedades, logo é uma propriedade.
* Processo de equilíbrio à
pressão constante
Þ
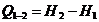
* A
entalpia é uma propriedade de um sistema e, é
encontrada em tabelas.
*
Entalpia por unidade de massa (Propriedade
extensiva) – Entalpia específica
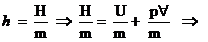
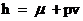
4.4 Calor Latente:
É a quantidade de energia que, transferida na
forma de calor, à pressão constante, conduz à
mudança de fase.
O calor latente é igual a variação da entalpia
de uma substância entre as condições de
saturação de duas fases.
O calor necessário para derreter uma unidade de
massa de uma substância à pressão constante é o
calor de fusão. E é igual a hsl = hl
– hs , na qual hs é
a entalpia do sólido saturado e hl
é a entalpia do líquido saturado.
O calor latente de vaporização é aquele
necessário para vaporizar completamente uma
unidade de massa de um líquido saturado. Esse
calor é igual a hlg = hg
– hl . Quando um sólido muda de fase
diretamente para o estado gasoso, ocorre a
sublimação. O calor de sublimação é hsg
= hg – hs.
O calor de fusão e o de sublimação são
relativamente insensíveis a mudanças de pressão
e temperatura. Para o gelo, o calor de fusão é
aproximadamente 330 kJ/kg e calor de sublimação
é cerca de 2040kJ/kg. O calor de vaporização da
água hlg é muito sensível à pressão e
à temperatura e se encontram em tabelas.
4.5 Primeira Lei aplicada a Sistemas:
A) Processo à
Temperatura Constante
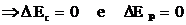

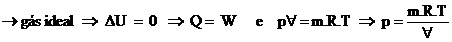

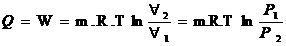
B) Processo a Volume
Constante
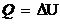
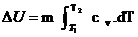
Gás ideal

C) Processo à Pressão
Constante
Quase-Estático
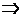 Q
=
Q
= 
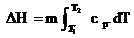
D) Processo Adiabático
Q = 0

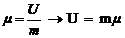



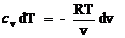

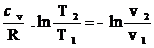
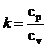
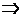

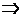

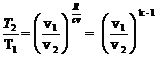
*
Processo Adiabático
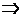 Caso
Particular do Processo Politrópico onde
Caso
Particular do Processo Politrópico onde
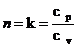
P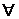 n
= Cte
n
= Cte
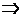

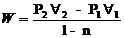
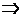

* Não
troca calor com a vizinhança.
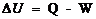
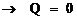
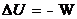
exercícios - Lista 4
1. Um automóvel de massa
igual a 1200 kg viaja a 75 km/h e colide, em um
acidente, com uma caminhonete de peso igual a
2500 kg que se encontra parada. Como resultado
final, a velocidade do automóvel é reduzida para
15 km/h, antes de parar totalmente. Da mesma
forma, a caminhonete atinge a velocidade de 10
km/h, também antes de parar totalmente. Calcule
a variação da energia interna, considerando
ambos os veículos como o sistema. (
U3 = - 20 kJ.
Quanto vale o trabalho para o segundo processo e
qual o trabalho líquido do ciclo? (30 kJ e 35 kJ)
5. Um tanque de 0,5 m3
contem ar (k = 1,4, R = 0,286 kJ/kgK) na pressão
de 7,0 MPa e 250 ºC, estando perfeitamente
isolado da vizinhança. Uma válvula é aberta e o
ar é descarregado até que a pressão dentro do
tanque caia para 400 kPa. Desconsiderando todas
as possíveis perdas por atrito e outras
irreversibilidades, como primeira aproximação,
calcule a massa de ar descarregada do tanque.
(20,4 kg)
6. Um gás está confinado
por uma divisória em um dos lados de um
reservatório rígido e termicamente isolado. O
outro lado da divisória está inicialmente
evacuado. Sabe-se que a condição inicial do gás,
CO2, considerado gás perfeito, é dada pela
pressão de 400 kPa, temperatura de 400 ºC,
ocupando o volume de V = 0,050 m3. Quando a
divisória é retirada, o gás se expande de forma
a ocupar todo o volume do reservatório. A
pressão de equilíbrio é 100 kPa. Determine a
variação de energia interna do processo e o
volume final, em m3.
(zero, 0,2 m3)

7. Um gás ideal ocupa um
volume de 0,5 m3 à temperatura de 340 K e dada
pressão. O gás realiza um processo isobárico até
que a temperatura caia para 290 K. Determine:
a) o volume final; (0,246
m3)
b) o trabalho realizado se
a pressão for 120 kPa; (- 8,9 kJ)
c) o calor trocado,
considerando que o calor específico a volume
constante seja igual a 0,52 kJ/kg.K e a massa
seja 1 kg.(- 34,9 kJ)
8. Ar na pressão de 140 kPa
e temperatura igual a 280 K, massa igual a 0,13
kg, está contido em um recipiente adiabático
como mostrado na figura abaixo. O sistema recebe
cerca de 18,3 kJ de trabalho no eixo pelas pás.
A temperatura final é igual a 420 K. Encontre o
calor trocado, o trabalho mecânico, o trabalho
total, as variações de energia interna, de
entalpia. (zero, 5,226 kJ,