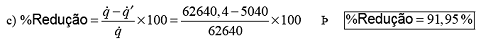TRANSFERÊNCIA DE CALOR POR CONVECÇÃO

Trata-se da transmissão de calor que ocorre entre um corpo sólido (principalmente) e um fluido em movimento, podendo o corpo fluido ser líquido ou gasoso. A convecção pode ser natural ou forçada. Diz-se que a convecção é natural quando o movimento do fluido ocorre unicamente devido a variações de seu peso específico (densidade). Na convecção forçada o movimento do fluido é provocado por uma bomba, no caso de um líquido, ou por um ventilador, no caso de um fluido gasoso.

A transferência de calor por convecção pode ser classificada de acordo com a natureza do escoamento:

Convecção livre (ou natural): ocorre devido às diferenças de densidade causadas por variações de temperatura no fluido.

            Convecção Forçada: quando o escoamento é causado por meios externos, tais como ventilador, uma bomba, etc.

            Convecção com mudança de fase: quando apresenta a troca de calor latente. Essa troca de calor latente é, geralmente, associada à mudança de fase entre os estados líquidos e vapor do fluido, condensação e ebulição.

Convecção natural	Convecção forçada
Escoamento induzido por forças de impulsão	Fluido forçado a escoar sobre superfície

6.3.1 Lei Básica

O calor transferido por convecção, na unidade de tempo, entre uma superfície e um fluido, pode ser calculado através da relação proposta por Isaac Newton:

                                           (eq. 1.21)

 A tabela a seguir fornece ordens de grandeza do coeficiente de película (h).

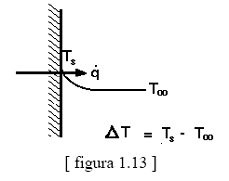
A figura 1.13 ilustra o perfil de temperatura para o caso de um fluido escoando sobre uma superfície aquecida.

A simplicidade da equação de Newton é ilusória, pois ela não explícita as dificuldades envolvidas no estudo da convecção. O coeficiente de película é, na realidade, uma função complexa do escoamento do fluido, das propriedades físicas do meio fluido e da geometria do sistema. A partir da equação 1.21, podem ser obtidas as unidades do coeficiente de película. No sistema métrico, temos:

   (eq.1.22)

Analogamente, nos sistemas Inglês e Internacional, temos:

6.3.2 Camada Limite

Quando um fluido escoa ao longo de uma superfície, seja o escoamento em regime laminar ou turbulento, as partículas na vizinhança da superfície são desaceleradas em virtude das forças viscosas. A porção de fluido contida na região de variação substancial de velocidade, ilustrada na figura 1.14, é denominada de camada limite hidrodinâmica.

Consideremos agora o escoamento de um fluido ao longo de uma superfície quando existe uma diferença de temperatura entre o fluido e a superfície. Neste caso, o fluido contido na região de variação substancial de temperatura é chamado de camada limite térmica. Por exemplo, analisemos a transferência de calor para o caso de um fluido escoando sobre uma superfície aquecida, como mostra a figura 1.15. Para que ocorra a transferência de calor por convecção através do fluido é necessário um gradiente de temperatura (camada limite térmica) em uma região de baixa velocidade (camada limite hidrodinâmica).

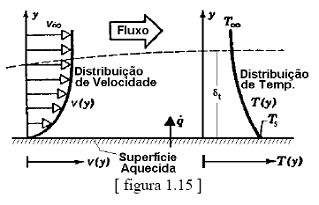
O mecanismo da convecção pode então ser entendido como a ação combinada de condução de calor na região de baixa velocidade onde existe um gradiente de temperatura e movimento de mistura na região de alta velocidade. Portanto:

· Região de baixa velocidade  => a condução é mais importante

· Região de alta velocidade     => a mistura entre o fluido mais quente e o mais frio é mais importante.

6.3 Resistência térmica na convecção.

Como visto anteriormente, a expressão para o fluxo de calor transferido por convecção é:

Um fluxo de calor é também uma relação entre um potencial térmico e uma resistência:

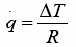
Igualando as equações obtemos a expressão para a resistência térmica na convecção:

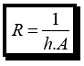    (eq. 1.26)

 

6.3.4 -Mecanismos Combinados de Transferência de Calor (Condução-Convecção)

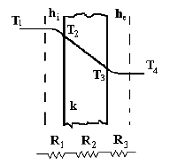
Consideremos uma parede plana situada entre dois fluidos a diferentes temperaturas. Um bom exemplo desta situação é o fluxo de calor gerado pela combustão dentro de um forno, que atravessa a parede por condução e se dissipa no ar atmosférico.

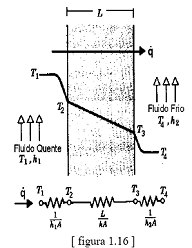
Utilizando a equação de Newton (equação 1.21) e a equação para o fluxo de calor em uma parede plana (equação 1.3), podemos obter as seguintes equações para o fluxo de calor transferido pelo forno:

Colocando as diferenças de temperatura em evidência e somando membro a membro, obtemos:

Substituindo as expressões para as resistências térmicas à convecção e à condução em parede plana na equação acima, obtemos fluxo de calor transferido pelo forno:

 

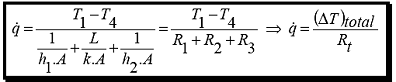  (eq. 1.27)

Portanto, também quando ocorre a ação combinada dos mecanismos de condução e convecção, a analogia com a eletricidade continua válida; sendo que a resistência total é igual à soma das resistências que estão em série, não importando se por convecção ou condução.

Exercício R.6.3.3. A parede de um edifício tem 30,5 cm de espessura e foi construída com um material de k = 1,31 W/m.K. Em dia de inverno as seguintes temperaturas foram medidas: temperatura do ar interior = 21,1 ºC; temperatura do ar exterior = -9,4 ºC; temperatura da face interna da parede = 13,3 ºC; temperatura da face externa da parede = -6,9 ºC. Calcular os coeficientes de película interno e externo à parede.

                            

 

Exercício R.6.3.4. Um reator de paredes planas foi construído em aço inox e tem formato cúbico com 2 m de lado. A temperatura no interior do reator é 600 ºC e o coeficiente de película interno é 45 kcal/h.m².ºC. Tendo em vista o alto fluxo de calor, deseja-se isola-lo com lã de rocha (k= 0,05 kcal/h.m.ºC) de modo a reduzir a transferência de calor. Considerando desprezível a resistência térmica da parede de aço inox e que o ar ambiente está a 20ºC com coeficiente de película 5 kcal/h.m².ºC, calcular :

a) O fluxo de calor antes da aplicação do isolamento;

b) A espessura do isolamento a ser usado, sabendo-se que a temperatura do isolamento na face externa deve ser igual a 62 ºC;

c) A redução (em %) do fluxo de calor após a aplicação do isolamento.