6.2.2
Condução de Calor em uma Parede Plana.
Consideremos a
transferência de calor por condução através de
uma parede plana submetida a uma
diferençam de temperatura. Ou seja, submetida a
uma fonte de calor, de temperatura constante e
conhecida, de um lado, e a um sorvedouro de
calor do outro lado, também de temperatura
constante e conhecida. Um bom exemplo disto é a
transferência de calor através da parede de um
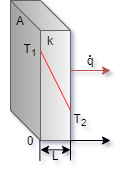
forno, como pode ser visto na figura abaixo, que
tem espessura L, área transversal A
e foi construído com material de
condutividade térmica k. Do lado de
dentro a fonte de calor mantém a temperatura na
superfície interna da parede constante e igual a
T1 e externamente o sorvedouro
de calor ( meio ambiente ) faz com que a
superfície externa permaneça igual a T2.
Aplicado a
equação de Fourier, tem-se:
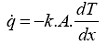(eq. 1.2)
Na figura 1.7
vemos que na face interna (x=0) a temperatura é
T1 e na face externa ( x=L ) a temperatura é T2.
Para a transferência em regime permanente o
calor transferido não varia com o tempo. Como a
área transversal da parede é uniforme e a
condutividade k é um valor médio, a integração
da equação 1.2, entre os limites que podem ser
verificados na figura 1.7, fica assim:
Considerando que
(T1 - T2) é a diferença de
temperatura entre as faces da parede (DT ), o
fluxo de calor a que atravessa a parede plana
por condução é :
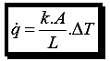(eq.
1.3)
Para melhor
entender o significado da equação 1.3
consideremos um exemplo prático. Suponhamos que
o engenheiro responsável pela operação de um
forno necessita reduzir as perdas térmicas pela
parede de um forno por razões econômicas.
Considerando a equação 1.3, o engenheiro tem,
por exemplo, as opções listadas na tabela 1.3:
Trocar a parede
ou reduzir a temperatura interna podem ações de
difícil implementação; porém, a colocação de
isolamento térmico sobre a parede cumpre ao
mesmo tempo as ações de redução da condutividade
térmica e aumento de espessura da parede.
Exercício
R.6.2.1.
Um equipamento
condicionador de ar deve manter uma sala, de 15
m de comprimento, 6 m de largura e 3 m de altura
a 22 ºC. As paredes da sala, de 25 cm de
espessura, são feitas de tijolos com
condutividade térmica de 0,14 Kcal/h.m.ºC e a
área das janelas podem ser consideradas
desprezíveis. A face externa das paredes pode
estar até a 40 ºC em um dia de verão.
Desprezando a troca de calor pelo piso e pelo
teto, que estão bem isolados, pede-se o calor a
ser extraído da sala pelo condicionador (em HP).
OBS: 1 HP =
641,2 Kcal/h
Para o cálculo
da área de transferência de calor desprezamos as
áreas do teto e piso, onde a transferência de
calor é desprezível. Desconsiderando a
influência das janelas, a área das paredes da
sala é:
A
= 2× 6 × 3 + 2
×(15× 3)= 126m2
Considerando que
a área das quinas das paredes, onde deve ser
levada em conta a transferência de calor
bidimensional, é pequena em relação ao resto,
podemos utilizar a equação 1.3:
6.2.3.
Analogia entre Resistência Térmica e Resistência
Elétrica
Dois sistemas
são análogos quando eles obedecem a equações
semelhantes. Por exemplo, a equação 1.3 que
fornece o fluxo de calor através de uma parede
plana pode ser colocada na seguinte forma:
(eq.
1.4)
O denominador e
o numerador da equação 1.4 podem ser entendidos
assim:
· (DT),
a diferença entre a temperatura da face quente e
da face fria, consiste no potencial que
causa a transferência de calor.
· (L /
k.A)
é equivalente a uma resistência térmica
(R) que a parede oferece à transferência de
calor.
Portanto, o
fluxo de calor através da parede pode ser
expresso da seguinte forma:
(eq.
1.5)
Se substituirmos
na equação 1.5 o símbolo do potencial de
temperatura
DT
pelo
de potencial elétrico, isto é, a diferença de
tensão
DU,
e o símbolo da resistência térmica R pelo
da resistência elétrica Re,
obtemos a equação 1.6 (lei de Ohm) para i,
a intensidade de corrente elétrica:
(eq.
1.6)
Dada esta
analogia, é comum a utilização de uma notação
semelhante a usada em circuitos elétricos,
quando representamos a resistência térmica de
uma parede ou associações de paredes. Assim, uma
parede de resistência R, submetida a um
potencial
DT e
atravessada por um fluxo de calor 
, pode
ser representada como na figura 1.8:
6.2.4.
Associação de paredes planas em série
Consideremos um
sistema de paredes planas associadas em série,
submetidas a uma fonte de calor, de temperatura
constante e conhecida, de um lado e a um
sorvedouro de calor do outro lado, também de
temperatura constante e conhecida. Assim, haverá
a transferência de um fluxo de calor contínuo no
regime permanente através da parede composta.
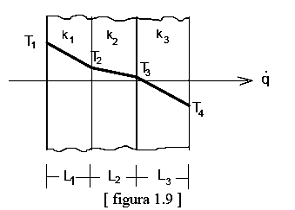
Como exemplo, analisemos a transferência de
calor através da parede de um forno, que pode
ser composta de uma camada interna de refratário
(condutividade k1 e espessura L1),
uma camada intermediária de isolante térmico
(condutividade k2 e espessura L2)
e uma camada externa de chapa de aço
(condutividade k3 e espessura L3).
A figura 1.9 ilustra o perfil de temperatura ao
longo da espessura da parede composta:
O fluxo de calor
que atravessa a parede composta pode ser obtido
em cada uma das paredes planas individualmente:
(eq.
1.7)
Isolando as
diferenças de temperatura em cada uma das
equações 1.7 e somando membro a membro, obtemos:
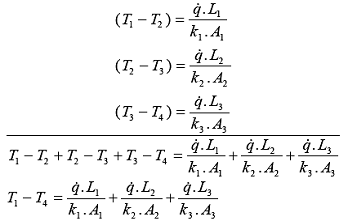(eq. 1.8)
Colocando em
evidência o fluxo de calor
e
substituindo os valores das resistências
térmicas em cada parede na equação 1.8, obtemos
o fluxo de calor pela parede do forno:
(eq. 1.9)
Portanto, para o
caso geral em que temos uma associação de
paredes n planas associadas em série o
fluxo de calor é dado por:
(eq.1.10)
6.2.5.
Associação de paredes planas em paralelo
Consideremos um
sistema de paredes planas associadas em
paralelo, como na figura 1.10, submetidas a
uma diferença de temperatura constante e
conhecida. Assim, haverá a transferência de um
fluxo de calor contínuo no regime permanente
através da parede composta.
·Todas
as paredes estão sujeitas a mesma diferença de
temperatura;
·As
paredes podem ser de materiais e/ou dimensões
diferentes;
·O fluxo
de calor total é a soma dos fluxos por cada
parede individual.
O fluxo de calor
que atravessa a parede composta pode ser obtido
em cada uma das paredes planas individualmente:
(eq.
1.11)
(eq. 1.12)
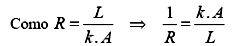
(eq. 1.13)
Portanto, para o
caso geral em que temos uma associação de n
paredes planas associadas em paralelo o
fluxo de calor é dado por:
(eq. 1.14)
Em uma
configuração em paralelo, embora se tenha
transferência de calor bidimensional, é
frequentemente razoável adotar condições
unidimensionais. Nestas condições, admite-se que
as superfícies paralelas à direção x são
isotérmicas. Entretanto, a medida que a
diferença entre as condutividades térmicas das
paredes ( k1 - k2 )
aumenta, os efeitos bidimensionais tornam-se
cada vez mais importantes.
Exercício
R.6.2.2.
Uma camada de material refratário (k=1,5
kcal/h.m.ºC) de 50 mm de espessura está
localizada entre duas chapas de aço (k = 45
kcal/h.mºC) de 6,3 mm de espessura. As faces da
camada refratária adjacentes às placas são
rugosas de modo que apenas 30 % da área total
está em contato com o aço. Os espaços vazios são
ocupados por ar
(k=0,013 kcal/h.m.ºC) e a espessura média da
rugosidade de 0,8 mm.
Considerando que
as temperaturas das superfícies externas da
placa de aço são 430 ºC e 90 ºC,
respectivamente; calcule o fluxo de calor que se
estabelece na parede composta. OBS: Na
rugosidade, o ar está parado (considerar apenas
a condução).
O circuito
equivalente para a parede composta é:
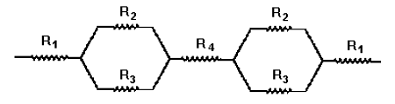
Cálculo das
resistências térmicas (para uma área unitária):
A resistência
equivalente à parede rugosa (refratário em
paralelo com o ar) é:
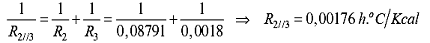
A resistência
total, agora, é obtida por meio de uma
associação em série:
Exercícios:
1- Uma casa de
10m x 14 m é construída sobre uma laje de
concreto de 12 cm de espessura. Qual é a taxa de
perda de calor através da laje se a temperatura
do solo é 5ºC, enquanto que no interior da casa
está a 22ºC.?
2- Uma caixa
cúbica com 20 cm de lado é construída com
painéis de concreto de 1,2 com de espessura. Uma
lâmpada de 100W é colocada dentro da caixa,
lacrada. Qual será a temperatura do ar dentro da
caixa quando a luz estiver acesa se a
temperatura do ar circundante é 20ºC?
3- As
superfícies interna e externa de uma janela de
vidro de 0,5 cm de espessura e área de 2m x 2m
no inverno tem 10ºC e 3ºC respectivamente.
Considerando que a condutividade térmica do
vidro é de 0,78 W/m.K, determine a perda de
calor através do vidro ao longo de um período de
5h. Qual seria sua resposta se a espessura do
vidro fosse 1,0 cm?
4- A parede
norte de uma casa aquecida eletricamente tem 6m
de comprimento, 3m de altura e 0,3 de espessura
e é construída com tijolos cuja condutividade
térmica e k = 0,72 W/m. K. Em uma noite de
inverno, as temperaturas interna e externa da
parede são medidas em torno de 17ºC e – 4ºC,
respectivamente, por um período de 8 horas.
Determine (a) a taxa de perda de calor por meio
da parede naquela noite e (b) o custo da perda
de calor para o proprietário da casa,
considerando que o custo da eletricidade é de R$
0,68 kWh.
5- Um medidor de
fluxo de calor fixado na superfície interna da
porta de uma geladeira de 3 cm de espessura
indica fluxo de calor de 32 W/m² por meio da
porta. As temperaturas das superfícies interna e
externa da porta são 7ºC e 15ºC,
respectivamente. Determine a condutividade
térmica média da porta da geladeira.
6- Uma janela
cuja área é de 2,0 m² é envidraçada com vidro de
espessura 4,0 mm. A janela está na parede de uma
casa e a temperatura externa é de 10ºC. A
temperatura no interior da casa é 25ºC. (a)
Quanta energia é transferida através da janela
em 1,0 h?
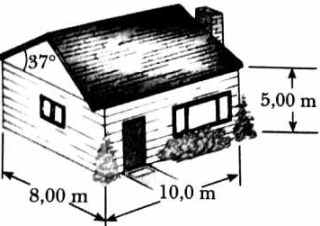
7- A
condutividade média das paredes (incluindo as
janelas) e do telhado da casa é de 0,480 W/m.ºC
e sua espessura média é 21 cm. A casa é aquecida
com gás natural tendo calor de combustão (isto
é, energia fornecida por metro cúbico de gás
queimado) de 9 300 kCal/m³. Quantos metros
cúbicos de gás devem ser queimados a cada dia
para manter a temperatura interna de 25ºC, se a
temperatura externa é de 0,0ºC? Desconsidere a
radiação perdida por meio do solo.
Clique aqui
para visualizar a resolução dos exercícios.
