5 - segunda lei da
termodinâmica
5.1 Máquinas Térmicas
Dispositivo que operam em um ciclo
termodinâmico.
A) Motor Térmico:
Máquina térmica cuja função é realizar trabalho.
|
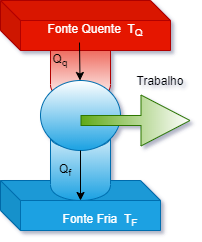 |
- Trabalho
efetivo útil:

- Eficiência:
 |
B) Bomba de calor:
Máquina térmica cuja função é adicionar calor
para um corpo ou sistema.
- Coeficiente de performance:

C) Refrigerador:
Máquina térmica cuja função é retirar calor de
um corpo ou sistema.
|
 |
- Coeficiente de
performance:
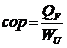
|
5.2 Enunciados da segunda
Lei da termodinâmica
A) Enunciado de
Clausius: “É impossível construir um
dispositivo que opere ciclicamente produzindo
somente o efeito de transferir calor de uma
fonte a baixa temperatura para outra fonte a
alta temperatura”.
B) Enunciado de Kelvin - Planck:
“É impossível para qualquer dispositivo que
operar em um ciclo termodinâmico receber energia
por transferência de calor de um único
reservatório térmico e produzir unicamente uma
quantidade resultante de trabalho (efeito de
elevar um peso) sobre sua vizinhança”.
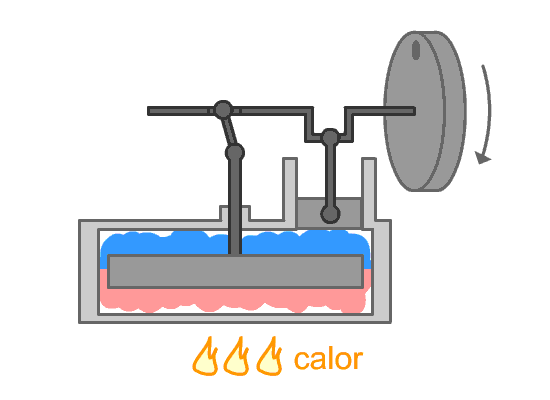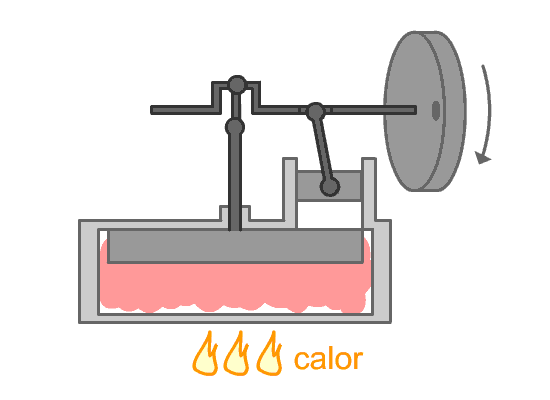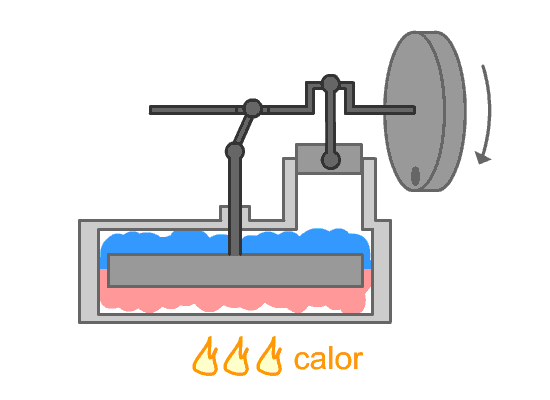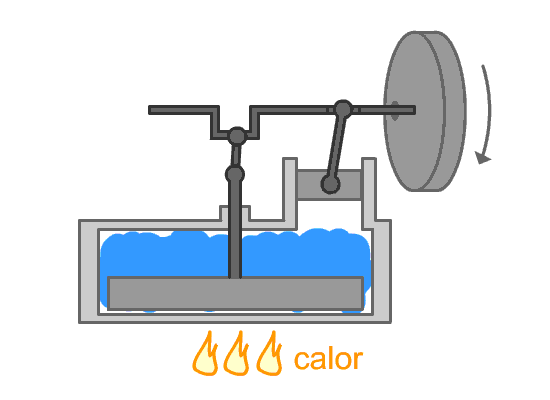
5.3 Processo reversível
Um processo que pode ser revertido e, quando
isso ocorre, não causa mudança definitiva no
sistema e nem na vizinhança.
Observe que a definição de processo
reversível se refere tanto ao sistema como à
vizinhança. O processo obviamente tem de ser um
processo de quase-equilíbrio, o que requer
condições adicionais:
1º) não há atrito envolvido no
processo;
2º) a transmissão de calor ocorre
provida por uma diferença de temperatura
infinitesimal;
3º) não ocorre expansão não
resistiva.
5.4 Maquina de Carnot
A máquina que opera mais eficientemente entre um
reservatório de temperatura mais alta outro de
temperatura mais baixa é chamada Máquina de
Carnot. Essa é uma máquina ideal que usa somente
processos reversíveis em seu ciclo de operação.
É uma máquina reversível.
A Máquina de Carnot é muito útil, já
que sua eficiência estabelece a máxima
eficiência possível de uma máquina térmica real
que opere entre as mesmas temperaturas.
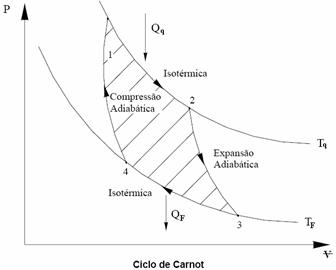
O Ciclo de Carnot demonstra que o maior rendimento possível para uma
máquina térmica é o de uma máquina que
realizasse um ciclo de duas transformações
adiabáticas e duas transformações isotérmicas,
alternadas entre si, de acordo com o esquema
abaixo.
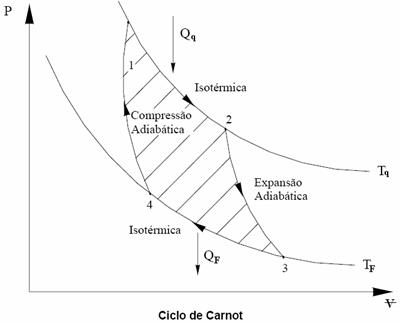
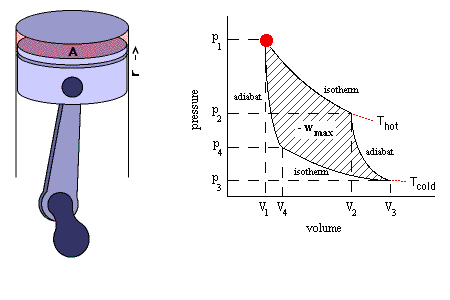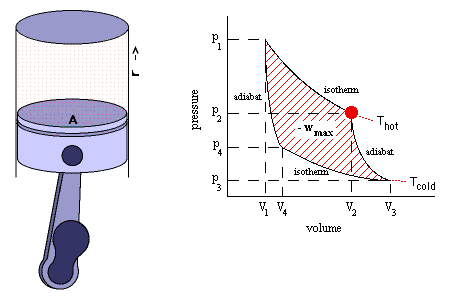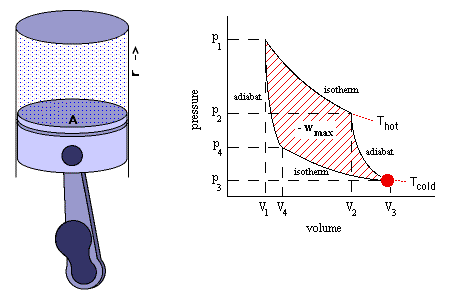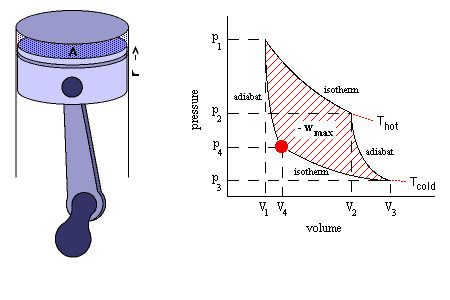

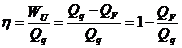
Considere uma máquina de Carnot reversível
operando segundo os ciclos descritos
anteriormente. A quantidade
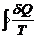 é
a integral cíclica do calor transmitido dividido
pela temperatura absoluta na qual a transmissão
de calor ocorre. Já que a temperatura Tq
é constante durante a transmissão de calor Qq
e TF é constante durante a
transmissão de calor QF, a integral
dada por
é
a integral cíclica do calor transmitido dividido
pela temperatura absoluta na qual a transmissão
de calor ocorre. Já que a temperatura Tq
é constante durante a transmissão de calor Qq
e TF é constante durante a
transmissão de calor QF, a integral
dada por
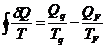
na qual o calor de QF que sai da
máquina de Carnot é considerado como positivo.
Podemos ver que, para o ciclo de Carnot,
 ou
ou
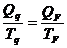
Substituindo na equação
anterior, concluímos

Logo, a quantidade
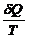 é
um diferencial exato, uma vez que a sua integral
cíclica é zero. Deixamos esse diferencial
perfeito ser denotado por
é
um diferencial exato, uma vez que a sua integral
cíclica é zero. Deixamos esse diferencial
perfeito ser denotado por
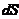 ,
na qual S representa uma função
escalar que depende somente do estado do sistema
e da quantidade de massa. Isso, na verdade,
qualifica S como uma propriedade
extensiva do sistema. Chamaremos essa
propriedade extensiva de entropia;
seu diferencial será dado por
,
na qual S representa uma função
escalar que depende somente do estado do sistema
e da quantidade de massa. Isso, na verdade,
qualifica S como uma propriedade
extensiva do sistema. Chamaremos essa
propriedade extensiva de entropia;
seu diferencial será dado por

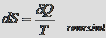
Isso pode ser integrado ao
longo de um processo para dar
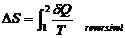
- a variação da entropia para um processo
reversível pode ser tanto positiva quanto
negativa, dependendo se o calor é adicionado ou
retirado do sistema durante o processo.
- para um processo adiabático reversível (Q =
0), a variação da entropia é zero.
- se o processo é irreversível e ao mesmo tempo
adiabático, não podemos afirmar que
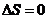 .
.
5.6 Desigualdade de
Clausius
O primeiro passo na análise da propriedade
termodinâmica que chamamos entropia é o
estabelecimento da desigualdade de Clausius, que
é
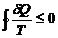
Onde a igualdade
prevalece para os ciclos reversíveis e a
desigualdade para os ciclos irreversíveis.
A desigualdade de Clausius é válida
para todos os ciclos possíveis, incluindo os
motores térmicos e os refrigeradores reversíveis
e irreversíveis.
OBS1:
- Postulado 1 – É impossível construir
uma máquina térmica operando entre dois
reservatórios de temperaturas dadas que seja
mais eficiente que a máquina de Carnot.
- Postulado 2 – A eficiência da máquina
de Carnot não depende da substância trabalhante
ou de qualquer característica do projeto da
maquina.
- Postulado 3 - Todas as máquinas
reversíveis, operando entre dois reservatórios a
temperaturas dadas, têm eficiências máximas
iguais.
|
|
1®2:
Expansão isotérmica reversível a Tq
Qq :
calor fornecido ( > 0 )
Þ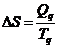
2®3:
Expansão adiabática reversível
Þ
não há troca de calor
Þ
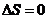
3®4:
Compressão isotérmica reversível a TF
QF :
calor cedido ( < 0 )
Þ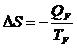
4®1:
Compressão adiabática reversível
Þ
não há troca de calor
Þ
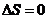
|
 como
como
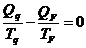 então
então
 .
.
O rendimento, como foi mostrado anteriormente é
dado por
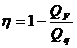 ,
podemos concluir que o rendimento máximo é
dado por
,
podemos concluir que o rendimento máximo é
dado por
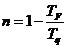
OBS 2: A máquina de Carnot, quando
operando ao inverso, funciona como uma bomba de
calor ou como um refrigerador, dependendo do
efeito desejado.
- Bomba de calor:

- Refrigerador de
Carnot:

OBS 3:
O principio do aumento de
entropia pode ser simplificado:
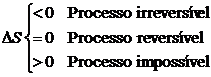
Esta
relação serve de critério para determinar a
natureza do processo.
O princípio do aumento da
entropia estabelece que a entropia aumentará até
atingir uma valor máximo, alcançando o sistema
uma estado de equilíbrio.
O segundo princípio da
termodinâmica também pode se enunciado em função
da entropia:
“A entropia do Universo
aumenta em todos os processos naturais”
EXEMPLOS:
exercícios - Lista 5
1. Sob que condições uma
máquina térmica ideal seria 100 % eficiente?
2. Por que um carro faz
menos quilômetros por litro de gasolina no
inverno do que no verão?
3. Quando um processo pode
ser considerado reversível? Os processos
naturais podem se reversíveis? O que ocorre com
a entropia do universo?
4. Ocorre variação da
entropia em movimentos puramente mecânicos?
5. Duas amostras de um gás,
inicialmente à mesma temperatura e pressão, são
comprimidas de volume V para o volume V/2, uma
isotermicamente e a outra adiabaticamente. Em
qual dos casos a pressão final é maior? A
entropia do gás varia durante qualquer um dos
processos?
6. Para fazer gelo, um
freezer extrai 42 kcal de calor de um
reservatório a - 12 ºC em cada ciclo. O
coeficiente de performance do freezer é 5,7. A
temperatura do ambiente é 26 ºC.
a) Qual a quantidade de
trabalho por ciclo necessário para manter o
freezer em funcionamento? (7,37 kcal)
b) Quanto calor, por ciclo,
é rejeitado para o ambiente? (49,37 kcal)
7. Um motor de Carnot opera
entre duas fontes de temperaturas a 200 ºC e 20
ºC, respectivamente. Se o trabalho desejado for
de 15 kJ, determine a transmissão de calor do
reservatório de temperatura mais alta e a
transmissão de calor para o reservatório de
temperatura mais baixa. (39,42 kJ, 24,42 kJ)
8. Um refrigerador está
resfriando um espaço a -5 ºC transferindo calor
para a atmosfera que está a 20 ºC. O objetivo é
reduzir a temperatura no espaço para -25 ºC.
Calcule a percentagem mínima de aumento no
trabalho necessário, assumindo o refrigerador de
Carnot, para a mesma quantidade de calor
removida. (94%)
9. Um refrigerador de
coeficiente de desempenho igual à metade de um
refrigerador de Carnot opera entre reservatórios
às temperaturas de 200K e 400K, absorvendo
6,3.105J de calor. Qual a quantidade de calor
rejeitada? (1,89.106J)
10. Uma máquina de Carnot’
reversível opera com 1kmol de gás monoatômico.
Durante a expansão isotérmica o volume dobra. A
razão do volume final para o inicial na expansão
adiabática é 5,7. O trabalho fornecido pela
máquina é 8,5.106 J em cada ciclo. Calcule as
temperaturas dos reservatórios.
11. Um mol de gás
monoatômico é levado através de um ciclo fechado
abca, conforme figura. Fazendo pb = 10 atm, Vb =
5,6.10-2 m3, Vc = 0,112m3. a) Calcule o calor
fornecido ao gás, o calor cedido pelo gás e o
rendimento do ciclo. b) Qual o rendimento
máximo? (5,9.104 J; -4,54.104 J; 23,2%; 68,5%)

12. Um inventor desenvolveu
um sistema de refrigeração que mantém o espaço
interno a uma temperatura de -15 ºC enquanto que
o ambiente externo está a 28 ºC. De acordo com
as informações fornecidas, o coeficiente de
performance é igual a 8,5. Avalie.
13. Uma máquina de Carnot
recebe cerca de 60 kW de energia da fonte de
alta temperatura, enquanto rejeita 120 MJ de
energia por hora para uma fonte fria cuja
temperatura é de 25 ºC. Determine a temperatura
da fonte quente e a potência da máquina. (263,5
ºC)
14. Num ciclo de Carnot, a
expansão isotérmica de um gás ideal acontece a
400 K e a compressão isotérmica a 300 K. Durante
a expansão, 500 cal de calor são transferidas
pelo gás. Calcule:
a) o trabalho realizado
pelo gás durante a expansão térmica; (2093 J)
b) o calor rejeitado pelo
gás durante a compressão isotérmica; (1570 J)
c) o trabalho realizado
pelo gás durante a compressão isotérmica. (1570
J)
Clique aqui
para acessar a resolução dos exercícios