Encontra-se na natureza um
material denominado magnetita, ou oxido de ferro
(Fe3 04) que possui a
propriedade de atrair limalhas de ferro e outros
objetos feitos com o mesmo material. Essa
interação entre a magnetita e a limalha de ferro
se manifesta à distância e, por essa razão,
dizemos que foi estabelecida uma ação de campo
ou que foi criado um campo magnético. Todo o
corpo capaz de criar influência magnética é
chamado ímã.
A magnetita é chamada ímã
natural, porque possui magnetismo natural, isto
é, o seu magnetismo é inerente à sua própria
natureza. Existem, entretanto, outras
substâncias que podem adquirir magnetismo
artificialmente, e são conhecidas como
substâncias ferromagnéticas. Entre elas,
estão ferro, o aço e o níquel.
O ferro, por exemplo, é
facilmente magnetizado, mas perde também com
rapidez ou magnetismo. Já o aço é difícil
magnetização, mas conserva bastante bem essa
propriedade.
Verifica-se, também, o que
é uma ímã apresenta duas regiões distintas, onde
a influência magnética se manifesta mais
acentuadamente, e que são chamados pólos do ímã.
Nestes pólos, batizado de norte e sul, a limalha
de ferro se concentra em maior densidade,
notando-se uma reprodução entre pólos de mesmo
nome e uma atração entre pólos de nomes
propostos.
Observa-se, ainda, que os
pólos norte é sul de um imã são inseparáveis,
isto é, se quebrarmos um ímã, teremos dois ímãs
completos. As figuras que se seguem ilustram o
que foi dito.
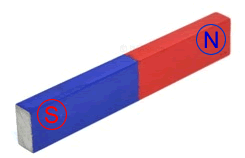

Um ímã, neste caso em
forma de barra, apresenta duas regiões
distintas, chamadas pólo norte e pólo sul.
Se dividirmos ou irmã em duas ou mais partes,
teremos sempre novos e mais completos.
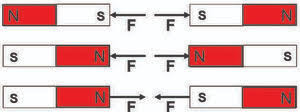
Pólos de mesmo nome
se repelem e pólos de nomes distintos se atraem.
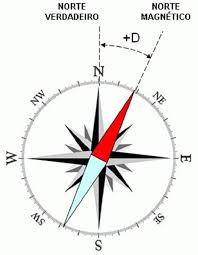
O magnetismo terrestre
É um fato
conhecido por todos nós que os primeiros
navegadores se orientavam os mares utilizando as
estrelas como referência e, ainda, um pequeno
engenho, o que conhecemos como bússola. Uma
bússola nada mais é do que uma agulha imantada,
que pode girar livremente sobre uma haste o que
aponta sempre em uma mesma direção, a menos que
outros irmãos estejam em sua proximidade. Os
Navegantes puderam orientar-se pelos mares,
graças ao magnetismo da Terra. Ela se comporta
como gigantesco ímã natural, verifica-se que o
pólo norte geográfico é um sul magnético e o
pólo sul geográfico é um Pólo Norte magnético.
Por esta razão, a
agulha imantada de uma bússola se orienta
segundo a influência magnética da Terra: o Pólo
Norte da agulha aponta para o norte geográfico, que é um sul magnético que o
pólo sul da agulha aponta para o sul geográfico, o que é, na realidade o
norte magnético.
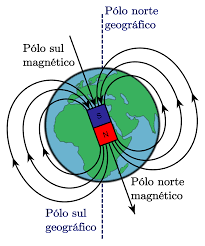
Agulha imantada de uma bússola
se orienta segundo a influência magnética da
Terra.
O campo magnético
Do mesmo modo que o campo
gravitacional é definido pelo vetor g (a
celebração da gravidade) e o campo elétrico
definido pelo vetor E o campo magnético pode ser
definido pelo vetor B, cujas características
descrevemos a seguir:
Campo magnético:
É um
campo de natureza vetorial.
Podem ser
estabelecidas linhas de indução as linhas de
indução. As linhas de indução saem do pólo norte e penetram no
pólo
sul, na região exterior ao irmã, mas, no
interior desse ímã, dirige-se do pólo sul para o
Pólo Norte.

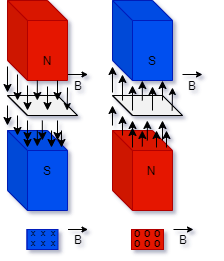
Linha de de indução de um campo magnético
reproduzir por uma irmã de forma prismática.
Linhas de indução de um
campo magnético produzido por uma irmã em forma
de U. Entre os pólos, o campo é uniforme.
Agulha de uma bússola
se orienta segundo a direção do campo magnético

Nas figuras, vemos que as linhas de indução de
dois ímãs. Note-se que a agulha da bússola se orienta
segundo essas linhas.
O vetor campo magnético B
é tangente à linha de indução no ponto
considerado.
O campo magnético é mais
intenso onde a densidade de linhas de indução é
maior.
As linhas de indução de um campo magnético
constante são paralelas igualmente espaçadas.
Determinação da intensidade do campo magnético.
A
experiência mostra que um campo magnético pode
exercer influência sobre uma partícula
eletricamente carregada, e que penetra com
determinada velocidade nesse campo. Essa
influência se manifesta pelo aparecimento, na
partícula, deu uma força, cuja direção é sempre
perpendicular ao plano formado pelo vetor
campo magnético e pelo vetor de velocidade da
partícula.
É por essa razão por que não podemos
chamar as linhas de campo magnético de linhas
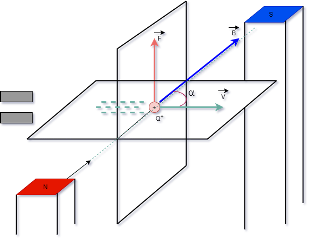
de força. A figura que se segue mostra uma das
linhas de indução de um campo magnético
constante, é uma partícula carregada
positivamente penetrando com velocidade v,
segundo um ângulo
a, nesse campo.
Observe que a
força magnética F é perpendicular ao
plano que contem v e B.
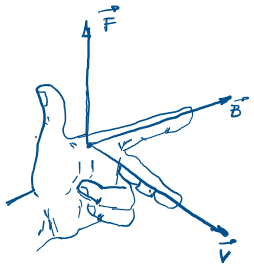
Regra da mão esquerda.
Ao penetrar com velocidade
v em uma região onde existe um campo magnético
B, uma carga Q fica sob a ação de uma força F
perpendicular ao plano formado por B e v. O
sentido dessa força é fornecido pela regra da
mão esquerda:
Operacionalmente, o módulo
do vetor B pode ser determinado em função das
grandezas carga, força e velocidade, pela
relação:
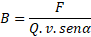 que podemos escrever:
que podemos escrever:
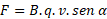
A unidade de B, no
sistema MKS , será:
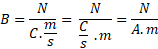 A
unidade
A
unidade
 foi
batizada de tesla, em homenagem a Nikola Tesla,
físico iugoslavo que nasceu em 1857, na
cidade de Smilijan, e faleceu em 1943, nos
Estados Unidos.
foi
batizada de tesla, em homenagem a Nikola Tesla,
físico iugoslavo que nasceu em 1857, na
cidade de Smilijan, e faleceu em 1943, nos
Estados Unidos.
A unidade de campo
magnético N/Am é também conhecida como weber/m2
. Temos, então, N/Am = Wb/m2
Quando uma
partícula, de massa m e carregada eletricamente
em uma carga Q+, penetra
perpendicularmente (a = 90º) em relação ao
vetor B, o movimento dessa partícula deixa de
ser retilíneo uniforme a passa ser circular
uniforme,devido a ação da força magnética F.
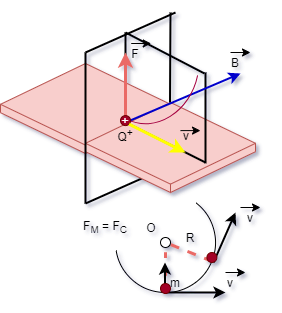
Note-se
que a força magnética Fm é a
força centrípeta do movimento circular uniforme.
O raio do M.C.U. pode ser calculado:
 a
= 90o => sen
a
= 1
a
= 90o => sen
a
= 1
FM= B.Q.v
FM
= Fc =>
m.v2 / R = B.Q.v
===> R = m.v/BQ

Para partículas carregadas
negativamente, a força magnética muda de
sentido, conservando a direção e o módulo


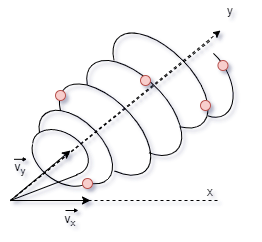
A figuras acima ilustram o movimento de uma
partícula positiva, ao penetra obliquamente em
um campo magnético. A trajetória é uma hélice
cilíndrica.
Temos:
A componente vx = v sen
a,
é a responsável pelo aparecimento da força
magnética Fm = B.Q.v sen
a, que produz
o movimento circular uniforme.
A componente vy = v cos
a
é a
responsável pelo movimento retilíneo uniforme,
de translação, em relação ao eixo y. A
combinação desses dois movimentos produz a
trajetória real da partícula.
Observe que, se a partícula for lançada ao longo
da direção do vetor B, teremos
a =
0o ou
a =
180o. Em ambos os casos, sendo sen
a
= 0 não
haverá força magnética na partícula.
F B.Q.v sen
a
a
= 0o => sen 0o = 0 = > F = 0
Com a intenção de facilitar a identificação
geométrica do vetor B, quando a ilustração
bidimensional dos vetores B v e F, adotaremos a
seguinte convenção: x o vetor B penetra na folha
do plano e O o vetor B sai da folha do plano.

Exercícios:
1) Uma partícula carregada, positivamente com
uma carga elétrica igual 2.10-6C,
penetra com velocidade de 4,0.103 m/s
em uma região do espaço onde existe um campo
magnético de indução igual a 5.10-2T.
Determinar o módulo da força magnética na carga,
supondo que:
a) o ângulo entre V e B vale 30º;
b) o ângulo entre V e B valo 90º.
2) Admitindo-se o exercício anterior e
considerando-se que a partícula tenha massa
igual a 6,0.10-12 kg, determinar no
caso de a = 90o;
a) o raio da trajetória circular;
b) a aceleração centrípeta.
3) Uma partícula de massa 2,0.10-14
kg e carga elétrica de 6,0.10-8C,
penetra com velocidade igual a 8,0.10 4
m/s em um campo magnético de indução B
= 7,0.10 -2 T,
perpendicular ao plano da folha, como mostra a
figura. Determinar:
a) o vetor força magnética que, inicialmente,
atua sobre a partícula;
b) a posição do ponto X, onde a partícula atinge
a placa;
c) a aceleração centrípeta do movimento;
d) o tempo gasto pela partícula para percorrer
OX.

Exercícios
propostos
1- Uma carga elétrica de
3.10 -8 C penetra com velocidade de
2.104 m/s em uma região onde existe
um campo magnético de intensidade 2.10-3
T. Determinar o módulo da força magnética na
carga, admitindo-se:
a)
a
= 45o ;
b)
a
= 90o ;
c)
a
= 180o ;
2- Uma partícula de
massa 2. 10-12 kg e carga 4,0.10-8
C penetra a 90o em um campo magnético
de 5,0.10-2 Wb/ m2 e
apresenta uma força magnética de intensidade
8,0.10-6 N. Determinar:
a) o módulo da velocidade
com que a partícula foi lançada;
b) o valor do raio da
trajetória da partícula;
c) a aceleração da
partícula.
3- Uma partícula de massa
3,0.10-14 kg e carga igual a 1,2.10-10
C é lançada, perpendicularmente, sobre as linhas
de indução de um campo magnético de intensidade
1,5 T, com velocidade de 2,0.103 m/s.
Determinar:
a) o módulo da força
magnética na partícula;
b) o raio de sua
trajetória;
c) a aceleração;
d) o período do movimento.
4- Uma partícula eletrizada
com carga de 2,0.10-3C entra
perpendicularmente em um campo magnético
uniforme de 0,20 Wb/m2, animada com
velocidade de 5,0.102 m/s. Determinar
a intensidade da força magnética que atua sobre
a partícula.
5- Um elétron é lançado
perpendicularmente a um campo magnético uniforme
de intensidade 0,5 Wb/m2, e descreve
uma trajetória circular de raio igual a 15 cm.
Sabendo-se que a carga do elétron é de 1,6.10-19
C, pode-se concluir que o módulo de sua
quantidade de movimento, em Ns, será:
a) 4,8.10-18
b) 1,2.10-20
c) 3,6.10-19
d) 5,4.10-21
e) 3,2.10-15
6- Um elétron com
energia cinética 20 eV (elétron-volt) penetra
perpendicularmente em um campo magnético
uniforme de intensidade 10-4 tesla. O
raio da circunferência descrita por ele é de:
a) 0,15 m
b) 0,36 m
c) 1,50 m
d) 3,60 m
e) n.d.a.
Dados carga do elétron
1,6.10-19 C
massa do elétron 9,1.10-31
kg
1 eV = 1,6.10-19
J
EFEITO
MAGNÉTICO DA CORRENTE ELÉTRICA - EXPERIÊNCIA DE
OERSTED
Sabemos que uma carga
elétrica sofre determinada influência, que se
manifesta através da presença de uma força, ao
ser lançada obliquamente em relação às linhas de
indução de um campo magnético.
Oersted mostrou, utilizando
uma experiência simples, que também as cargas
elétricas em movimento, e, portanto, uma
corrente elétrica, podem produzir efeitos
magnéticos.
Verificação experimental
Título: A experiência de
Oersted.
Objetivo: Verificação
experimental dos efeitos magnéticos de uma
corrente elétrica.
Material:
Bússola
amperímetro
gerador
fios
chave
Montagem:
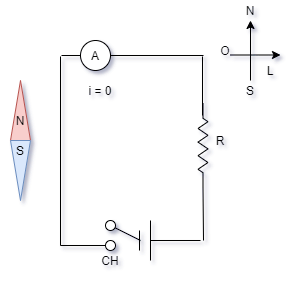
Procedimentos:
1- Monte o circuito
simples, indicado na figura, tendo o cuidado de
orientar o fio AB de modo que a agulha da
bússola fique direcionada segundo o campo
magnético da Terra. Essa orientação não é
obrigatória, mas facilita a observação do
fenômeno.
2- Com a chave (CH) aberta,
não há presença de corrente elétrica e a agulha
da bússola se mantém alinhada segundo o campo
magnético da Terra.
3- Ligando-se a chave, fica
estabelecida uma corrente elétrica ao logo do
circuito, e verifica-se que a agulha da bússola
se movimenta e, após algum tempo, entra em
repouso, mas orientada, agora, em outra direção.
Essa nova direção é a direção do campo magnético
resultante da combinação entre o campo magnético
da Terra e o campo magnético produzido pela
corrente elétrica transportada pelo fio.
Aumentando-se a intensidade
da corrente, pode-se aumentar o campo magnético
artificial, de modo que a agulha se oriente,
praticamente, apenas em relação a esse campo
artificial.

Conclusão:
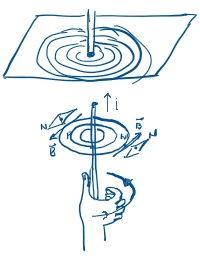
1. Toda corrente elétrica
produz, na sua vizinhança, um campo magnético
cujas linhas de indução são círculos
concêntricos, tendo como eixo central o fio que
transporta a corrente. Este fato pode ser
verificado, espalhando-se limalha de ferro sobre
um suporte de papel conforme mostra a figura.
2. O vetor campo magnético
é tangente a essas linhas de indução e a agulha
da bússola se orienta segundo essa direção.
3. Operacionalmente, a
intensidade do campo magnético em um ponto
situado a uma distancia r do fio pode ser
calculada pela relação matemática conhecida como
Lei de Biot-Savart.

onde :
i = intensidade de corrente
elétrica transportada pelo fio;
r = distância do fio ao
ponto considerado, ou raio da linha de indução
que contem o ponto;
C = constante que depende
do meio no qual o fio esta imerso.
C (vácuo ou ar ) = 10
-7 N/ A2
4. Sendo a corrente
elétrica um movimento de cargas, fica evidente
que todo carga elétrica em movimento sofre
efeitos de campos magnéticos e produz, também,
na sua vizinhança, um campo magnético.
Isso significa que, entre
duas cargas elétricas em movimento, aparecem
duas forças: a de origem eletrostática, derivada
da lei de Coulomb, e a de natureza magnética,
devida aos campos produzidos pelas cargas.
Consequências:
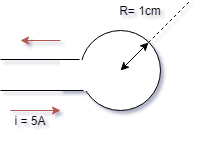
1. Campo magnético no
centro de uma espira circular.
A figura que se segue
mostra um fio condutor trabalhado, de modo que
adquiriu a forma circular.
Um condutor desse formato é
denominado espira circular.
Os terminais desse condutor
(espira) se encontram ligados a um gerador, de
modo que circula no conjunto uma corrente de
intensidade i. Levando-se em consideração a
experiência de Orested, é fácil concluir que a
corrente elétrica produz, ao longo desse fio, um
campo magnético, cujas linhas de indução podem
ser obtidas utilizando-s a regra da mão direita.

A corrente elétrica que
circula por uma espira produz, no seu centro, um
campo magnético.
A experiência mostra que,
no centro da espira, fica estabelecido um campo
magnético resultante, cuja intensidade pode ser
calculada pela relação seguinte, decorrente da
aplicação da lei e Biot - Savart.

Admitindo-se, por exemplo,
que a espera tenha um raio de 0,30 m e que a
leitura do amperímetro seja 12 A, no centro da
espira teremos um campo magnético de intensidade
igual a:
 ==>
==>
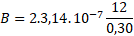 ==>
==> 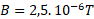
2- Campo magnético em um
solenóide.
Chama-se solenóide todo
condutor enrolado de modo a formar um grupo de
espiras circulares e consecutivas.
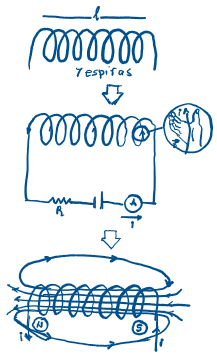
Um solenóide, percorrido
por uma corrente elétrica, produz, na sua
vizinhança, efeitos magnéticos se
transforma, ele mesmo, em um ímã.
Ligando-se os terminais do
solenóide a um gerador, uma corrente elétrica
percorrerá suas espiras e um campo magnético
será estabelecido na sua vizinhança.
Admitindo-se o mesmo artifício da mão direita,
pode-se determinar a direção das linhas de
indução do campo magnético produzido no seu
interior. Para pontos internos, agastados das
extremidades,o campo magnético é praticamente
constante e, aplicando novamente a lei de
Biot-Svart, sua intensidade pode ser calculada
pela equação:
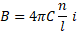
onde n é o número de
espirar e l o comprimento do solenóide.
Admitindo-se, por exemplo,
a corrente elétrica de 12 A, o comprimento igual
0,20 m e 7 espiras, a intensidade do campo no
interior do solenóide será de:



EXERCÍCIOS RESOLVIDOS
1) A figura mostra um fio retilíneo, muito
comprido e percorrido por uma corrente elétrica
de intensidade 12 A.
 a)
determinar a intensidade do campo magnético em
dois pontos M e N, distantes do fio,
respectivamente 30 cm e 10 cm.
a)
determinar a intensidade do campo magnético em
dois pontos M e N, distantes do fio,
respectivamente 30 cm e 10 cm.
b) como seria o gráfico B x X?
c) qual o raio da linha de indução onde B =
6,0.10-5 T?
d) qual a corrente que o fio deve transportar
para que o campo, no ponto M, tenha intensidade
igual a B= 3,6.10-4 T?
2) Uma espira tem raio igual a 20 cm,
resistência própria igual a 3,0
W e faz parte do circuito esquematizado
na figura abaixo.

a) a corrente que sai da bateria
b) a intensidade do campo magnético no seu
centro
c) a f. e. m., do gerador, necessária para
produzir, no seu centro, um campo magnético de
intensidade B= 5,4. 10-5 T.
3) Um solenóide possui 80 espiras enroladas em
um comprimento de 12 cm. Sabendo-se que circula
por ele uma corrente de 18 A, determinar:
a) A intensidade do campo magnético no seu
interior
b) o número de espiras necessárias para que o
campo magnético no seu interior alcance o valor
de B= 5,6. 10-2 T. , com a mesma
corrente.
GABARITO
TESTES:
1V; 2F;
3F; 4V; 5V; 6F; 7V; 8V; 9V; 10V.
1E; 2D;
3E; 4B; 5E; 6C; 7D; 8D.
Teste e problemas (Magnetismo)
Assinale com V as afirmações verdadeiras e com F
as afirmações falsas.
1. ( ) Campo magnético é uma região do
espaço modificada pela presença de um imã ou de
um fio condutor percorrido por corrente elétrica
ou por um corpo eletrizado em movimento.
2. ( ) Um corpo eletrizado pode originar
isoladamente um campo elétrico ou um campo
magnético conforme esteja estacionário ou em
movimento, respectivamente.
3. ( ) A grandeza vetorial indução
magnética B caracteriza
quantitativamente o campo magnética, num ponto
da região do mesmo.
4. ( ) Num ponto do campo magnético
produzido pela corrente que percorre um fio
condutor longo e retilíneo, definimos a
intensidade da indução magnética B do
campo, como sendo o quociente entre as
intensidades da força magnética num elemento de
prova e do próprio elemento de prova.
5. ( ) De acordo com o teste anterior , B
depende de Fm e de iDs.
6. ( ) De acordo com o teste número 4, o
vetor indução magnética B tem a direção
da força magnética.
8. ( ) A intensidade da indução magnética
no S. I. é o tesla (T).
9. ( ) Uma agulha imantada colocada na
região de um campo magnético orienta-se na
direção de B, estando o seu pólo sul no
sentido de B.
10. ( ) A linhas de indução de um imã
nascem no pólo norte e morrem no pólo sul.
11. ( ) No caso de um fio condutor longo e
retilíneo, percorrido por uma corrente elétrica,
as linhas de indução do campo magnético por ele
originado são circunferências de centro no fio e
cujo sentido pode ser obtido pela "regra da mão
direita".
13. ( ) A indução magnética B, originada
pelo elemento de corrente iDs
e por P.
14. ( ) Nas condições do teste anterior B
é diretamente proporcional a iDs
e ao angulo entre B e
Ds e inversamente
proporcional ao quadrado da distância entre P e
o elemento de corrente.
15. ( ) A indução magnética B
originada pela corrente i que percorre uma
espira circular de raio R, em seu centro O, é
perpendicular ao plano da espira, sendo
diretamente proporcional a i e inversamente
proporcional a R.
16. ( ) A lei circuital de Àmpere diz que
a circuitação da indução magnética em um
percurso fechado é proporcional à soma algébrica
das intensidades de correntes enlaçadas.
17. ( ) A intensidade da indução magnética
originada por um solenóide reto e longo, nos
pontos de seu interior, longe das extremidades,
é diretamente proporcional à corrente que
percorre o mesmo e ao número de espiras por
unidade de comprimento.
18. ( ) Denomína-se linha isógona toda
linha tal que a inclinação magnética é a mesma
em todos os seus pontos.
19. ( ) Equador magnético é a isóclina em
cujos pontos a inclinação é nula e coincide com
o equador geográfico.
20. ( ) Pólos magnéticos da Terra são
pontos da superfície da mesma nos quais temos
inclinação magnética i = 90º, estando os mesmos
próximos aos pólos geográficos de nome oposto.
GABARITO: 1V; 2F; 3V; 4V; 5F; 6F; 7V; 8V; 9F;
10F; 11F; 12V; 13F;
14F;
15V; 16V; 17V; 18F; 19F;
20V.
Problemas:
Obs.: Nesta série
de problemas , utilizaremos sempre o valo de
m0 = 4p.10-7T.m/A.
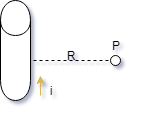
1- Um condutor reto e extenso é percorrido por
uma corrente elétrica constante de intensidade i
= 4A. Dê as características do vetor indução
magnética B no ponto P da figura, situado a uma
distância R = 2 cm do condutor.
2- Determina as características do vetor indução
magnética resultante no ponto P da figura.
.png)
3. Dê as características do vetor indução
magnética B, originado pela corrente elétrica i
no ponto 0 da figura.